Sunday, May 28, 2006
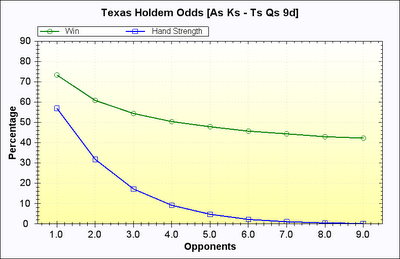
Probably the most frequent question I received after writing a poker article for CodeProject was "How do you calculate win odds for multiple opponents?"
Writing code to exhaustively calculate the win odds for multiple opponents is very straightforward; unfortunately the time it takes to calculate an answer is prohibitive.
There are solutions to this problem available on line. One solution is Hold'em Showdown by Steve Brecher. Hold'em Showdown is a very fast solution for exhaustively calculating win odds for multiple opponents. However, even using the fastest hand evaluator publicly available and tweaking C code for this specific solution, the maximum opponents is 4 and getting the results takes some time, making this technique not terrible practical for getting answers in real-time.
Another method is to use precalculated tables. An example of this is Marv742's tables. One problem with using tables is they are large (50Megs compressed). Another problem is that Marv's tables only have results for 1, 3, 5 and 9 opponents.
I know a online player that has made good use of Marv742's tables, but using them seemed very unwieldy and limiting to me.
An Alternate Approach
I prefer using a Monte Carlo approach to calculating win odds. This technique works well at getting good approximate values. The more time you allow for the calculation the more accurate the returned value. My experience is that 0.01 (10 milliseconds) give reasonably results. Of course more time gives even more accurate results.
I used this technique to create the graph in the beginning of this article. The results are very consistent and stable even using fairly small time values. You can use the same method I use by calling Hand.WinOdds() in the Hand Evaluator library found on the downloads section.
The following code shows how to use this technique to calculate approximate win odds for 5 opponents.
using System;
using HoldemHand;
// This example calculates the win odds for a player having "As Ks" against
// five random players
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
// Calculate win odds using example code
double w1 = WinOddsFivePlayerMonteCarlo(Hand.ParseHand("as ks"), 0UL, 5.0);
Console.WriteLine("win: {0:0.00}%, time {1:0.0000}", w1 * 100.0, 5.0);
// Calcluate win odds using Hand.WinOdds()
w1 = Hand.WinOdds(Hand.ParseHand("as ks"), 0UL, 5, 5.0);
Console.WriteLine("win: {0:0.00}%, time {1:0.0000}", w1 * 100.0, 5.0);
}
// An example of how to calculate win odds for five players
static double WinOddsFivePlayerMonteCarlo(ulong pocket, ulong board, double duration)
{
// Keep track of stats
long win = 0, lose = 0, tie = 0;
// Loop through random boards
foreach (ulong boardmask in Hand.RandomHands(board, pocket, 5, duration))
{
// Get random opponent hands
ulong opp1mask = Hand.RandomHand(boardmask | pocket, 2);
ulong opp2mask = Hand.RandomHand(boardmask | pocket | opp1mask, 2);
ulong opp3mask = Hand.RandomHand(boardmask | pocket | opp1mask |
opp2mask, 2);
ulong opp4mask = Hand.RandomHand(boardmask | pocket | opp1mask |
opp2mask | opp3mask, 2);
ulong opp5mask = Hand.RandomHand(boardmask | pocket | opp1mask |
opp2mask | opp3mask | opp4mask, 2);
// Get hand value for player and opponents
uint playerHandVal = Hand.Evaluate(pocket | boardmask);
uint opp1HandVal = Hand.Evaluate(opp1mask | boardmask);
uint opp2HandVal = Hand.Evaluate(opp2mask | boardmask);
uint opp3HandVal = Hand.Evaluate(opp3mask | boardmask);
uint opp4HandVal = Hand.Evaluate(opp4mask | boardmask);
uint opp5HandVal = Hand.Evaluate(opp5mask | boardmask);
// Tally results
if (playerHandVal > opp1HandVal &&
playerHandVal > opp2HandVal &&
playerHandVal > opp3HandVal &&
playerHandVal > opp4HandVal &&
playerHandVal > opp5HandVal)
{
win++;
}
else if (playerHandVal >= opp1HandVal &&
playerHandVal >= opp2HandVal &&
playerHandVal >= opp3HandVal &&
playerHandVal >= opp4HandVal &&
playerHandVal >= opp5HandVal)
{
tie++;
}
else
{
lose++;
}
}
// Return stats
return ((double)(win + tie / 2.0)) / ((double)(win + tie + lose));
}
}
}