Friday, June 16, 2006
Washington State recently enacted a law making online gambling a felony.
I grew up in Washington State, I was born in Spokane, went to college in Pullman Washington and had a student internship in Renton Washington. I moved to Oregon for my first job more than 20 years ago.
I hadn't been through the Seattle area since I first moved to Oregon, but last fall needed to drive to Spokane from Clatskanie Oregon. The fastest way there was through Seattle.
When I moved from Seattle years ago there were no Indian Casinos (just smoke shops and fireworks stands that occasionally blew up). Now there are more Casinos visible from the freeway than McDonald's restaurants.
Also in the last 20 years Washington State has adopted a state lottery. The Washington State lottery currently advertises regularly on TV along site online poker sites.
Don't Write About Gambling In Washington
Washington State officials have interpreted the new law very broadly. Not only is gambling online illegal but linking to online casinos, hosting online casino advertising, or even talking about gambling. The irony of these positions hasn't escaped the eye of the Seattle Times. In a recent article the Times states:
All that, says the state the ads, the linking, even the discussing violates a new state law barring online wagering or using the Internet to transmit "gambling information."
"It's what the feds would call 'aiding and abetting,' " says the director of the state's gambling commission, Rick Day. "Telling people how to gamble online, where to do it, giving a link to it that's all obviously enabling something that is illegal."
The articles author, Danny Westneat, goes on to say:
Gambling officials told me The Seattle Times may be afoul of the law because we print a poker how-to column, "Card Shark," by gambler Daniel Negreanu. He sometimes tells readers to hone their skills at online casinos. And at the end of each column is a Web address, fullcontactpoker.com, where readers can comment.
According to the Washington State Gaming Commission:
The Washington State Gambling Commission was created to keep the criminal element out of gambling and to protect the public. The recently enacted
legislation supports the Commission's efforts at fulfilling that responsibility.
But in one added twist, not all online gambling is illegal. In 2004 the Washington State Legislature passed a law to bet on horse races online if you place the bet with a state licensed firm.
So the bottom line is you can legal gambling in card rooms in Washington, you go to Indian Casinos, you can by Washington Lottery Tickets, and you can play the ponies online. But don't play poker online, link to any poker sites, or even talk about online gambling on your website if you live in Washington.
Apparently online Casinos are putting the pinch on the states lively hood. Don't get in the way of the governor and his tax revenue, at least not in Washington.
Thursday, June 08, 2006
You probably remember covering Permutations and Combinations in your High School math class. In case you missed that day of school, here's a quick summary.
Permutations are used when you care about order. For example, As Ks would be considered unique from Ks As. Combinations are used when order doesn't matter.
In Texas Holdem the hole cards As Ks (the ace of spades and the king of spades) are considered equivalent to Ks As. So combinations are used when calculating the number of hands.
The formula for combinations is nCk=n!/(k!*(n-k)!). To calculate the number of unique hole card combinations in Texas Holdem you substitute the following 52C2= 52!/(2!*(52-2)!) which is 1326 total hands.
In the Hand Evaluator library (available in the downloads area on the left), we use 52 bits of a 64 bit int as a hand mask. A hand mask describes a specific hand. Each of the 52 bits in the mask describe a specific card. When the bit is on the card is present. Combinations are used to describe the total number of possible unique hand masks.
The Hand Evaluator library also uses hand values. A hand value is the result of passing a hand mask into the Evaluate() method. What's returned is an integer value that can be used to determine which hands are of higher value than another.
So looking at the number of unique hand value is also an interesting thing to know. The following table shows the number of hand values, permutations and combinations (hand masks) that a hand of a specific number of cards requires.

The first time I saw anyone work through this was Cactus Kev. I found the results for 5 card hands to be, well, shocking. I never expected there to be only 7462 unique hand values for 5 card hands. Cactus Kev uses this fact to create a very fast hand evaluator algorithm.
What I found even more surprising (at least until I spent sometime thinking about it), was that 6 and 7 card hands have even fewer possible hand values.
Though this may seem like trivia, understanding this has been quite helpful to me. I hope it's useful for you.
Tuesday, June 06, 2006
I'm sure you've read a book or two on Holdem. One of the things I noticed while reading poker books is that there is a de facto standard for describing pocket cards. Most books use some variant of the following to describe pocket hands.
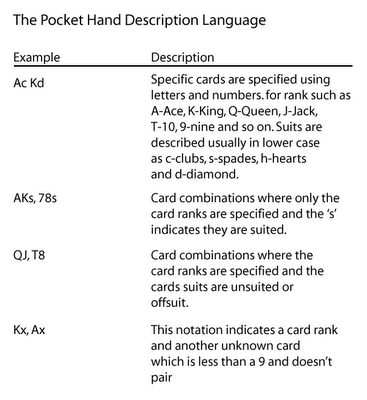
Most poker software that parse string representations of pocket hands only supports the first item in the de facto standard.
I've implemented a much richer query language. I support all of the common poker book syntax plus some extensions.
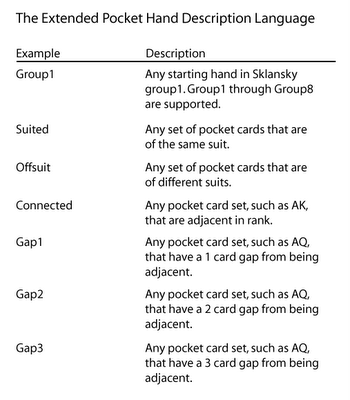
I've also added some operators.
 Why a Pocket Query Language?
Why a Pocket Query Language?
One of the things I've done too many times has been write code to analyze specific matchups. For example, have you ever wondered what the advantage is for have a suited connected verses a non-suited connector?
I'd guess you've probably wondered, but weren't enough of a masochist to write the code. On the other hand, I am enough of a masochist to write the code for many, many match ups. After awhile I decide I had enough of that and wrote a query language so that I could write my matchup analysis once and just put in query strings.
The following is an example of the result of using query strings rather than hard coded match ups. Oh and there is about a 5% advantage for suited connectors.
I've attempted to make it trivial to write analysis code that utilized Pocket Queries. Here's an example.
using System;
using System.Collections.Generic;
using System.Text;
using HoldemHand;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
// A Pocket Query Returns an array of all
// hands that meet the criterion.
ulong[] player1 = PocketHands.Query("Group3-Group5");
ulong[] player2 = PocketHands.Query("Axs");
// Holds stats
long player1Wins = 0, player2Wins = 0,
ties = 0, count = 0;
// Iterate through 10000 trials.
for (int trials = 0; trials < 10000; trials++)
{
// Pick a random pocket hand out of player1's query set
ulong player1Mask = Hand.RandomHand(player1, 0UL, 2);
// Pick a random pocket hand for player2
ulong player2Mask = Hand.RandomHand(player2, player1Mask, 2);
// Pick a random board
ulong boardMask = Hand.RandomHand(player1Mask |player2Mask, 5);
// Create a hand value for each player
uint player1HandValue = Hand.Evaluate(boardMask | player1Mask, 7);
uint player2HandValue = Hand.Evaluate(boardMask | player2Mask, 7);
// Calculate Winners
if (player1HandValue > player2HandValue)
{
player1Wins++;
}
else if (player1HandValue < player2HandValue)
{
player2Wins++;
}
else
{
ties++;
}
count++;
}
// Print results
Console.WriteLine("Player1: {0:0.0}%",
(player1Wins + ties/2.0) / ((double)count) * 100.0);
Console.WriteLine("Player2: {0:0.0}%",
(player2Wins + ties/2.0) / ((double)count) * 100.0);
}
}
}
Tuesday, May 30, 2006
Most Hold'em players know what Outs are. According to Wikipedia an out is:
[A]n out is any unseen card that, if drawn, will improve a player's hand to one that is likely to win
The question for the programmer is, is this definition sufficent to write a function that returns the cards that are outs?
Let's look at the two key points made by Wikipedia. They are:
- The hand must improve
- The new hand is likely to win.
Let's start by writing a function that meets the first criterion.
using System;
using HoldemHand;
// A first try at calculating outs
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
string pocket = "As Ac";
string board = "Kd 8h 9c";
// Calcuate the outs
ulong outsmask = Outs(Hand.ParseHand(pocket), Hand.ParseHand(board));
Console.WriteLine("[{0}] {1} : Outs Count {2}",
pocket, board, Hand.BitCount(outsmask));
// List the cards
foreach (string card in Hand.Cards(outsmask))
{
Console.Write("{0} ", card);
}
Console.WriteLine();
}
// Return a hand mask of the cards that improve our hand
static ulong Outs(ulong pocket, ulong board)
{
ulong retval = 0UL;
ulong hand = pocket board;
// Get original hand value
uint playerOrigHandVal = Hand.Evaluate(hand);
// Look ahead one card
foreach (ulong card in Hand.Hands(0UL, hand, 1))
{
// Get new hand value
uint playerNewHandVal = Hand.Evaluate(hand card);
// If the hand improved then we have an out
if (playerNewHandVal > playerOrigHandVal)
{
// Add card to outs mask
retval = card;
}
}
// return outs as a hand mask
return retval;
}
}
}
Passing this starting hand A♠ A♣, K♦ 8♥ 9♣ it into our new method returns the following outs:
- K♠, 9♠, 9♥, 8♠, K♥, 9♦, 8♦, K♣, 8♣ - Two pair
- A♥, A♦ - Trips
- Q♠, J♠, T♠, Q♥, J♥, T♥, Q♦, J♦, T♦, Q♣, J♣, T♣ - Improves Kicker
I think most people would agree that super-sizing your kicker probably doesn't help much here. I think most people would also agree that improving the board doesn't help either. So let's add two more rules:
- The hand must improve
- The new hand improvement must be better than an improved kicker
- The new combined hand must be stronger than the just the board
- The new hand is likely to win
The following example handle these new rules and allows opponent hands to be added.
using System;
using HoldemHand;
// A first try at calculating outs
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
string pocket = "As Ac";
string board = "Kd 8h 9c";
// Calcuate the outs
ulong outsmask = Outs(Hand.ParseHand(pocket), Hand.ParseHand(board));
Console.WriteLine("[{0}] {1} : Outs Count {2}",
pocket, board, Hand.BitCount(outsmask));
// List the cards
foreach (string card in Hand.Cards(outsmask))
{
Console.Write("{0} ", card);
}
Console.WriteLine();
}
// Return a hand mask of the cards that improve our hand
static ulong Outs(ulong pocket, ulong board, params ulong [] opponents)
{
ulong retval = 0UL;
// Get original hand value
uint playerOrigHandVal = Hand.Evaluate(pocket board);
// Look ahead one card
foreach (ulong card in Hand.Hands(0UL, board pocket, 1))
{
// Get new hand value
uint playerNewHandVal = Hand.Evaluate(pocket board card);
// Get new board value
uint boardHandVal = Hand.Evaluate(board card);
// Is the new hand better than the old one?
bool handImproved = playerNewHandVal > playerOrigHandVal &&
Hand.HandType(playerNewHandVal) > Hand.HandType(playerOrigHandVal);
// This compare ensures we move up in hand type.
bool handStrongerThanBoard =
Hand.HandType(playerNewHandVal) > Hand.HandType(boardHandVal);
// Check against opponents cards
bool handBeatAllOpponents = true;
if (handImproved && handStrongerThanBoard &&
opponents != null && opponents.Length > 0)
{
foreach (ulong opponent in opponents)
{
uint opponentHandVal = Hand.Evaluate(opponent board card);
if (opponentHandVal > playerNewHandVal)
{
handBeatAllOpponents = false;
break;
}
}
}
// If the hand improved then we have an out
if (handImproved && handStrongerThanBoard && handBeatAllOpponents)
{
// Add card to outs mask
retval = card;
}
}
// return outs as a hand mask
return retval;
}
}
}
Passing this starting hand A♠ A♣, K♦ 8♥ 9♣ to our new method produces following outs:
- K♠, 9♠, 9♥, 8♠, K♥, 9♦, 8♦, K♣, 8♣ - Two pair
- A♥, A♦ - Trips
This new method is certainly better than our first method. But we can still do better.
Stay tuned for more indepth discussion on improving our outs method.
Sunday, May 28, 2006

Probably the most frequent question I received after writing a poker article for CodeProject was "How do you calculate win odds for multiple opponents?"
Writing code to exhaustively calculate the win odds for multiple opponents is very straightforward; unfortunately the time it takes to calculate an answer is prohibitive.
There are solutions to this problem available on line. One solution is Hold'em Showdown by Steve Brecher. Hold'em Showdown is a very fast solution for exhaustively calculating win odds for multiple opponents. However, even using the fastest hand evaluator publicly available and tweaking C code for this specific solution, the maximum opponents is 4 and getting the results takes some time, making this technique not terrible practical for getting answers in real-time.
Another method is to use precalculated tables. An example of this is Marv742's tables. One problem with using tables is they are large (50Megs compressed). Another problem is that Marv's tables only have results for 1, 3, 5 and 9 opponents.
I know a online player that has made good use of Marv742's tables, but using them seemed very unwieldy and limiting to me.
An Alternate Approach
I prefer using a Monte Carlo approach to calculating win odds. This technique works well at getting good approximate values. The more time you allow for the calculation the more accurate the returned value. My experience is that 0.01 (10 milliseconds) give reasonably results. Of course more time gives even more accurate results.
I used this technique to create the graph in the beginning of this article. The results are very consistent and stable even using fairly small time values. You can use the same method I use by calling Hand.WinOdds() in the Hand Evaluator library found on the downloads section.
The following code shows how to use this technique to calculate approximate win odds for 5 opponents.
using System;
using HoldemHand;
// This example calculates the win odds for a player having "As Ks" against
// five random players
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
// Calculate win odds using example code
double w1 = WinOddsFivePlayerMonteCarlo(Hand.ParseHand("as ks"), 0UL, 5.0);
Console.WriteLine("win: {0:0.00}%, time {1:0.0000}", w1 * 100.0, 5.0);
// Calcluate win odds using Hand.WinOdds()
w1 = Hand.WinOdds(Hand.ParseHand("as ks"), 0UL, 5, 5.0);
Console.WriteLine("win: {0:0.00}%, time {1:0.0000}", w1 * 100.0, 5.0);
}
// An example of how to calculate win odds for five players
static double WinOddsFivePlayerMonteCarlo(ulong pocket, ulong board, double duration)
{
// Keep track of stats
long win = 0, lose = 0, tie = 0;
// Loop through random boards
foreach (ulong boardmask in Hand.RandomHands(board, pocket, 5, duration))
{
// Get random opponent hands
ulong opp1mask = Hand.RandomHand(boardmask | pocket, 2);
ulong opp2mask = Hand.RandomHand(boardmask | pocket | opp1mask, 2);
ulong opp3mask = Hand.RandomHand(boardmask | pocket | opp1mask |
opp2mask, 2);
ulong opp4mask = Hand.RandomHand(boardmask | pocket | opp1mask |
opp2mask | opp3mask, 2);
ulong opp5mask = Hand.RandomHand(boardmask | pocket | opp1mask |
opp2mask | opp3mask | opp4mask, 2);
// Get hand value for player and opponents
uint playerHandVal = Hand.Evaluate(pocket | boardmask);
uint opp1HandVal = Hand.Evaluate(opp1mask | boardmask);
uint opp2HandVal = Hand.Evaluate(opp2mask | boardmask);
uint opp3HandVal = Hand.Evaluate(opp3mask | boardmask);
uint opp4HandVal = Hand.Evaluate(opp4mask | boardmask);
uint opp5HandVal = Hand.Evaluate(opp5mask | boardmask);
// Tally results
if (playerHandVal > opp1HandVal &&
playerHandVal > opp2HandVal &&
playerHandVal > opp3HandVal &&
playerHandVal > opp4HandVal &&
playerHandVal > opp5HandVal)
{
win++;
}
else if (playerHandVal >= opp1HandVal &&
playerHandVal >= opp2HandVal &&
playerHandVal >= opp3HandVal &&
playerHandVal >= opp4HandVal &&
playerHandVal >= opp5HandVal)
{
tie++;
}
else
{
lose++;
}
}
// Return stats
return ((double)(win + tie / 2.0)) / ((double)(win + tie + lose));
}
}
}
Saturday, May 27, 2006
Using Monte Carlo Analysis In Poker Software
Monte Carlo Analysis can be used in analysing poker hands. There are many reasons people choose to use Monte Carlo Analysis. In poker, the most common reason is to get a quick answer for something that otherwise would take a prohibitively long-time to calculate.
I resisted using Monte Carlo Analysis for quite some time. I clung to my wish that a sufficently fast Poker Hand Evaluator Library would eliminate the need for needing to use woo-woo techniques like this.
To convince myself of the value of Monte Carlo Analysis I had to work through how to analyse the win odds for one or more players.
Calculating Win Odds
Consider the following code. It calculates the win odds for a player being dealt AKs against a random opponent.
This program takes about 299 seconds (nearly 5 minutes) to calculate with no board cards. That means the code is evaluating 14,084,025 Hands/Sec and a total of 2,097,572,400 (yes billions) of hand match ups. With three cards in the board it takes 0.263 seconds and a total of 1,070,190 hand match ups.
When there are cards on the board, this function is very usable. However, if you are calculating hole card win probabilities with this, then the algorithm is far too slow to be usable.
using System;
using System.Collections.Generic;
using HoldemHand;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
// This code calculates the probablity of As Ks winning against
// another random hand.
ulong pocketmask = Hand.ParseHand("As Ks"); // Hole hand
ulong board = Hand.ParseHand(""); // No board cards yet
long wins = 0, ties = 0, loses = 0, count = 0;
// Iterate through all possible opponent hole cards
foreach (ulong oppmask in Hand.Hands(0UL, board pocketmask, 2))
{
// Iterate through all board cards
foreach (ulong boardmask in Hand.Hands(board, pocketmask oppmask, 5))
{
// Evaluate the player and opponent hands and tally the results
uint pocketHandVal = Hand.Evaluate(pocketmask boardmask, 7);
uint oppHandVal = Hand.Evaluate(oppmask boardmask, 7);
if (pocketHandVal > oppHandVal)
{
wins++;
}
else if (pocketHandVal == oppHandVal)
{
ties++;
}
else
{
loses++;
}
count++;
}
}
// Prints: Win 67.0446323092352%
Console.WriteLine("Win {0}%",
(((double)wins) + ((double)ties) / 2.0) / ((double)count) * 100.0);
}
}
}
Getting "Good Enough" Results Quickly
I'm not a perfectionist and appearently neither are many of the successful professional Texas Holdem Players.
In Phil Gordon's Little Green Book (a very good book I might add) he describes a very simple heuristic that can be calculate in your head that give the approximate odds of hitting your "outs". He calls this "the rule of 4 and 2". The way this heuristic works is that you count your outs. If you've just seen the flop (and not the turn card) then multiply the outs by 4 and you will have the approximate percentage of hitting your outs. If you've seen the turn (but not the river) you multiply the outs by 2 to get the approximate odds of hitting your outs.
These types of simple estimates are used by many of the professional players to help evaluate their situation. If an estimate is good enough for them, then it's probably good enough for the rest of us -- if used correctly. Monte Carlo Analysis is just a method for a computer to quickly estimate the odds in a specific situation.
Consider our previous example. It would take 299 seconds to iterate through all the possible situations and give us an exact anwers.
The following table was calculated using Monte Carlo Analysis. The number on the left is the number of trials, the second number is the estimated win odds (the exact odds were 67.0446323092352%). The third column is the difference between the exact answer and the estimate answer. The fourth column is the time taken in seconds.

Notice at 0.0013 seconds (1.3 milleseconds) we have 3 good digits. At 0.007 (7 milliseconds) we have about 4 good digits. At 0.0357 (36 milliseconds) we have 5 good digits. It's easy to see that we can get very good estimates in well less than a second.
The following code was used to generate the previous table.
using System;
using System.Collections.Generic;
using System.Runtime.InteropServices;
using HoldemHand;
namespace ConsoleApplication1
{
class Program
{
[DllImport("Kernel32.dll")]
private static extern bool QueryPerformanceCounter(out long lpPerformanceCount);
[DllImport("Kernel32.dll")]
private static extern bool QueryPerformanceFrequency(out long lpFrequency);
static void Main(string[] args)
{
// This code calculates the probablity of As Ks winning against
// another random hand.
ulong pocketmask = Hand.ParseHand("As Ks"); // Hole hand
ulong board = Hand.ParseHand(""); // No board cards yet
// Trial numbers
int[] trialsTable = {
10, 50, 100, 500, 1000, 5000, 10000, 15000, 20000,
25000, 30000, 40000, 50000, 100000, 150000, 200000,
500000, 1000000, 2000000, 5000000, 10000000, 20000000
};
// timer values
long start, freq, curtime;
// Get time frequency
QueryPerformanceFrequency(out freq);
Console.WriteLine("Trials,Wins,Difference,Duration");
foreach (int trials in trialsTable)
{
long wins = 0, ties = 0, loses = 0, count = 0;
// Get start time
QueryPerformanceCounter(out start);
// Iterate through a series board cards
foreach (ulong boardmask in
Hand.RandomHands(board, pocketmask, 5, trials))
{
// Get a random opponent hand
ulong oppmask = Hand.RandomHand(boardmask | pocketmask, 2);
// Evaluate the player and opponent hands
uint pocketHandVal = Hand.Evaluate(pocketmask | boardmask, 7);
uint oppHandVal = Hand.Evaluate(oppmask | boardmask, 7);
// Calculate Statistics
if (pocketHandVal > oppHandVal)
{
wins++;
}
else if (pocketHandVal == oppHandVal)
{
ties++;
}
else
{
loses++;
}
count++;
}
// Get Current Time
QueryPerformanceCounter(out curtime);
double duration = ((curtime - start) / ((double)freq));
// Correct answer is 67.0446323092352%
Console.WriteLine("{0},{1},{2}%,{3}",
trials,
string.Format("{0:0.00}%",
(((double)wins) + ((double)ties) / 2.0) / ((double)count) *100.0),
string.Format("{0:0.0000}",
67.0446323092352 - ((((double)wins) +
((double)ties) / 2.0) / ((double)count) * 100.0)),
string.Format("{0:0.0000}", duration));
}
}
}
}
I use the functions QueryPerformanceFrequency
and QueryPerformanceCount
to get highly accurate time duration information for the table. The rest of the code should look very much like the program we used to exhaustively calculate the odds. However, you will notice two new methods. They are Hand.RandomHand() and Hand.RandomHands().
Monte Carlo Analysis Helper Methods
The following method is intentionally similar to the IEnumerable<ulong>
Hands(ulong shared, ulong dead,
int ncards) method.
One additional argument is added which is the number of random hands that are to be iterated through by this enumerator.
public static IEnumerable<ulong> Hand.RandomHands(ulong shared, ulong dead, int ncards, int trials)
This IEnumerable method, allows the foreach command to iterate through random hands. The hands returned must meet the criterion specified. The number of hands specified in the last argument are returned.
public static IEnumerable<ulong> Hand.RandomHands(ulong shared, ulong dead, int ncards, double duration)
This method is similar to the previous method. However, rather than specifying the number of trials, a time duration is specified. This allows a time budget to be specified for getting an answer. I have a mild preference to using this version of these methods.
static public ulong Hand.RandomHand(ulong shared, ulong dead, int ncards)
This method allows a random hand to be returned. It must meet the specified input criterion.
Hopefully this is enough to get you started with Monte Carlo Analysis.
Friday, May 26, 2006
Being able to easily and quickly enumerate through available poker hands is essential in doing any poker analysis. C# makes enumeration easy by providing the ablity to build methods that are used with the foreach language construct.
Iterating through hands simply requires toggling all of the possible 7 bit combinations for 7 card hands or 5 bit combinations for 5 card hands. To assist in this task, C# iterators can be used.
The following method can be used to iterate through all possible hands containing the number of cards specifed.
public static IEnumerable<ulong>
This next method is a little more elaborate. It allows a mask containing shared cards to be passed, along with a mask containing dead cards, and finally the number of cards to be returned.
Shared cards are cards that must be included in the returned mask, dead cards are cards that must not be included in the return mask
public static IEnumerable<ulong>
These methods provide and easy way to count up win/tie/lose stats to figure out what the odds are for a specific player/opponent/board match up. The following example shows how you can calculate such a matchup.
using System;
using System.Collections.Generic;
using System.Text;
using HoldemHand;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
// Keep stats
double win = 0.0, lose = 0.0, tie = 0.0;
// Parse cards into hand masks
ulong pocketcards = Hand.ParseHand("as ks");
ulong opponentcards = Hand.ParseHand("5h tc");
ulong boardcards = Hand.ParseHand("qs ts 5c");
// Loop through all remaining 5 card boards.
// All 5 card boardmask must contain the starting
// board cards. That's why boardcards is passed in the first argument.
// Neither player nor opponents cards should be allowed in the boardmask
// which is why they are ORed together and passed to Hand.Hands()
// second argument.
foreach (ulong boardmask in
Hand.Hands(boardcards, pocketcards | opponentcards, 5))
{
// Get Hand Values
uint playerhandval = Hand.Evaluate(pocketcards | boardmask);
uint opphandval = Hand.Evaluate(opponentcards | boardmask);
// Compare and update the stats
if (playerhandval > opphandval)
{
win += 1.0;
}
else if (playerhandval == opphandval)
{
tie += 1.0;
}
else
{
lose += 1.0;
}
}
// Print results which is 42.63%
Console.WriteLine("Odds of beating opponent {0:0.00}%",
(win + tie / 2.0) / (win + tie + lose) * 100.0);
}
}
}
